高等数学

Wang Haihua

🍈 🍉🍊 🍋 🍌

---

伯努利分布

定义

伯努利试验是一种随机试验，只有两种可能的结果，成功或失败，每次成功的概率都是相同的。伯努利分布是一个伯努利试验的离散分布。其概率可表示为 $$ P(X=x)= \begin{cases} p, & x=1 \\ 1-p,&x=0 \end{cases} $$ 这里$X$代表随机变量，$x$代表随机变量取值，$p$是试验成功的概率。

例子

将买一次彩票中奖或不中奖视为一次事件，就可以用伯努利分布来进行表示。

二项分布

定义

在n次独立重复的伯努利试验中，设每次试验中事件A发生的概率为p。用X表示n重伯努利试验中事件A发生的次数，则X的可能取值为0，1，…，n,且对每一个k（0≤k≤n）,事件{X=k}即为“n次试验中事件A恰好发生k次”，随机变量X的离散概率分布即为二项分布（Binomial Distribution）。

二项分布有四个特点:

• n 次相同的试验(trial)
• 每次试验要么“成功”要么“失败”
• 每次试验“成功”概率不变
• 试验之间相互独立(independent)

二项分布的概率质量函数(Probability mass function)为

\begin{equation} C_n^k p^k(1-p)^{n-k} \end{equation}

例子

我们拿一个简单的例子来看二项分布的概率质量函数

每个月，一个私人银行家可能会见50人询问贷款，根据经验，他们中的30%有不良信用记录。计算有不良信用记录的人的个数分别为1，2，...,50的概率。

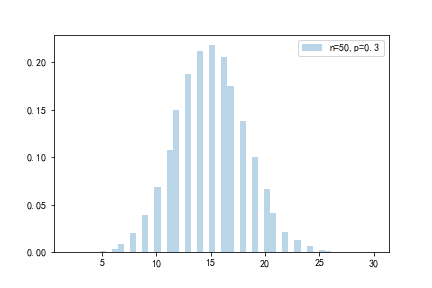
这个银行家恰巧碰到14个有不良贷款记录客户的概率是 \begin{equation} C_50^{14} 0.3^{14}(1-0.3)^{50-14} \approx 11.89% \end{equation}

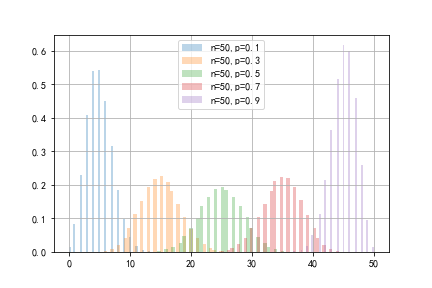
下图表示当p取0.1，0.3，0.5，0.7，0.9时的概率分布

泊松分布

泊松概率分布考虑的是在连续时间或空间单位上发生随机事件次数的概率。通俗的解释为：基于过去某个随机事件在某段时间或某个空间内发生的平均次数，预测该随机事件在未来同样长的时间或同样大的空间内发生n次的概率。泊松分布经常被用于销量较低的商品库存控制，特别是价格昂贵、需求量不大的商品。例如，某家海鲜酒楼在过去—年的时间里，每月平均卖出7只龙虾，如果该餐厅 希望今后能有95%的把握满足顾客的龙 虾需求，需要存储多少只龙虾呢？像这一类问题就能用泊松概率分布来解决。

当𝑛→∞和𝑝→0时，二项分布收敛于泊松分布，即当𝑛较大而𝑝较小时，可以用泊松来近似二项分布。 \begin{equation} P(X=k)=\frac{\lambda^ke^{-\lambda}}{k!} \end{equation}

例子

对于普通交易员来说，每笔交易遇到“黑天鹅”冲击的概率是1/1000，一个交易员每个月设置20笔交易，5年内遇到2笔“黑天鹅”的概率是多少? 这个问题可以用二项式法求解，公式如下

\begin{equation} \text{交易总次数} = 20\times 12\times 5=1200\\ P(x=2) = \binom{1200}{2}\Big(\frac{1}{1000}\Big)^2\Big(\frac{999}{1000}\Big)^{1198} \end{equation}

当然，我们可以用泊松分布来近似它，泊松分布的参数是

\begin{equation} \lambda = np = 1200 \times \frac{1}{1000} = 1.2 \end{equation}

也就是说，平均每5年就会出现1.2次黑天鹅事件。 \begin{equation} P(x=2)=\frac{\lambda^ke^{-\lambda}}{k!}=\frac{1.2^2e^{-1.2}}{2!} \end{equation}

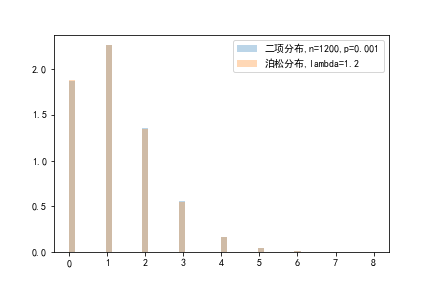
下图表示了随机生成10000个参数为n=1200，p=0.001的二项分布和参数为lambda=1.2的泊松分布的图像对比（请忽略y轴刻度）。

负指数分布

当事件的发生的次数服从泊松分布时，事件发生间隔时间服从负指数分布，负指数分布的概率密度函数为

$$ f(t)=\left\{\begin{array}{cc} {\lambda e^{-\lambda t},} & {t \geq 0} \\ {0,} & {t<0} \end{array}\right. $$

其中，$\lambda>0$与泊松分布参数相同，表示单位事件发生次数。

参考资料

• https://baijiahao.baidu.com/s?id=1703456602669206942&wfr=spider&for=pc
• https://zhuanlan.zhihu.com/p/77003855

---

import numpy as np
import matplotlib.pyplot as plt
import scipy as sp
import pandas as pd
import scipy.stats
plt.rcParams['font.family']=['SimHei']
plt.rcParams['axes.unicode_minus'] = False
%matplotlib inline

2.2

n = 50
p = .3
bad_credit = np.arange(1, 51)
y = sp.stats.binom.pmf(bad_credit, n, p)
fig, ax = plt.subplots(figsize = (10, 6))
ax.plot(bad_credit, y, lw = 3, color = 'r', alpha = .5)
ax.set_ylim([0, .13])
ax.set_title('1到50个人有不良信用记录的概率', size = 16, x = .5, y = 1.02)
ax.set_xlabel('有不良信用记录的人数', size = 12)
ax.set_ylabel('概率', size = 12)
plt.savefig('images/01bino.png')
plt.show()

x_bino0 =np.random.binomial(50,0.3,100000)
plt.hist(x_bino0,bins=50,alpha=0.3,density=True,label=f'n=50,p={0.3}')
plt.legend()
plt.savefig('images/01bino0.png')

for p in [0.1*i for i in range(1,10) if i%2==1]:
    x_bino = np.random.binomial(50,p,100000)
    plt.hist(x_bino,bins=50,alpha=0.3,density=True,label=f'n=50,p={round(p,1)}')
plt.grid()
plt.legend()
plt.savefig('images/01bino1.png')

泊松分布

x_bino2 =np.random.binomial(1200,0.001,100000)
x_poisson2 = np.random.poisson(1.2,100000)
plt.hist(x_bino2,bins=50,density=True,alpha=0.3,label=f'二项分布,n=1200,p=0.001')
plt.hist(x_poisson2,bins=50,alpha=0.3,density=True,label=f'泊松分布,lambda=1.2')
plt.legend()
plt.savefig('images/pro0103.png')